6. 二叉树1

5. 最长回文串

0417，mid
考点：动态规划、分类讨论

解法一：动态规划

分析：

动态规划的 dp：
dp[i][j] 表示 i~j 是一个回文串，此时赋值为 true： dp[i][j] = true;

判断当前 dp[i][j] 是否为一个回文串时，分析：

s[i] 和 s[j] 是否相等，如果相等，则：
1. 子串 dp[i+1][j-1] 是回文串，它就是回文串；
2. 反之，子串不是回文串，它就不是回文串
如果不相等，就一定不是回文串。

找到转换方程：

if (s[i] === s[j]) {
  dp[i][j] = dp[i-1][j+1];
  range = [x-1, y+1];
} else {
  dp[i-1][j+1] = false;
}

找到问题边界：

// 子串长度为1，肯定是一个回文串
for (let i = 0; i < len ; i++) {
  dp[i][i] = true;
}

// 字串长度为2，如果两个元素相等，也是一个回文串
for (let i = 0; i < len - 1 ; i++) {
  if (s[i] === [i+1])
    dp[i][i+1] = true;
}

求解：

var longestPalindrome = function (s) {
  // 特例
  if (!s || s.length === 0) return;
  const len = s.length;
  let range = [0, 0]

  // 初始化二维数组
  // dp[i][j] 表示s[i...j] 是否是回文串
  const dp = new Array(len)
  for (let i = 0; i < len; i++) {
    dp[i] = [];
  }

  // 处理边界:
  for (let i = 0; i < len; i++) {
    //n=1时，都是回文串
    dp[i][i] = true;
    if (i < len - 1 && s[i] === s[i + 1]) {
      // n=2时，两个元素相等也是回文串：'bb'
      dp[i][i + 1] = true;
      range = [i, i + 1]
    }
  }

  // n 为判断回文串的长度，从3开始
  for (let n = 3; n <= len; n++) {
    // 左下标
    for (let i = 0; i <= len - n; i++) {
      // 右下标
      let j = i + n - 1;
      if (dp[i + 1][j - 1]) {
        // 如果上一个是回文串，则判断当前下标是不是回文串
        if (s[i] === s[j]) {
          dp[i][j] = true;
          range = [i, j];
        }
      }
    }
  }

  return s.slice(range[0], range[1] + 1)
};

解法二：分类讨论

中心扩展算法

把每一个节点当成中心（中心是一个回文串）然后左右扩展，寻找以当前中心为基的最长回文串。

var longestPalindrome = function (s) {
  // 特殊情况
  if (!s || s.length === 0) return;
  
  const len = s.length;
  // range[0]和range[1]代表最长回文串的起始和终点坐标
  let range = [0, 0]

  // 遍历每一个数，把这个数当成回文串的中心，向左右方向扩展。
  for (let i = 0; i < len; i++) {
    estimate(i);
  }
  return s.slice(range[0], range[1] + 1);

  // 回文有两种：中心点是一个的单数(aba)，中心点是两个以上的双数(abba、abbba) 
  // 把回文串统一看成：中间部分+左右不分。中间部分全部是同一字符，左右部分对称相等
  function estimate(x) {
    let y = x;
    // 处理回文中间部分：连续相同字符
    while (y + 1 < len && s[y] === s[y + 1]) {
      y++
    }
    // 处理回文的左右两边：找到最长回文串
    while ( x - 1 >= 0 && y < len && s[x-1] === s[y+1]) {
      x--;
      y++;
    }
    // 判断当前找到的回文串和之前保存的回文串哪一个更长
    if (range[1] - range[0] < y - x) {
      range = [x, y];
    }
  }
};

犯错：

dp[i][j] = true 写成了 dp[i][j] === true，这个问题还看了很久没找到。

105. 从前序与中序遍历序列构造二叉树

从前序与中序遍历序列构造二叉树
0419、mid
动态规划，二叉树构造

1. 找特点

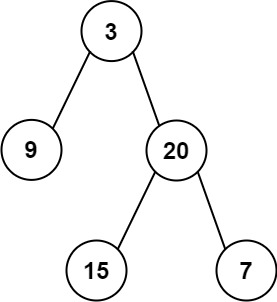
preorder = [3,9,20,15,7], 
inorder = [9,3,15,20,7]

前序遍历的特点：根、左、右。preorder[0] 就是根节点

中序遍历的特点：左、根、右。找到根节点后，左边的是左子树，右边的是右子树：

// 中序列表中，根的下标:
const index = inorder.indexOf(preorder[0]);
// 从中序列表中，找到左子树长度，右子树长度：
const leftLen = index
const rightLen = inorder.length - leftLen - 1;

2. 找思路

这样，可以根据下标切分出：

前序列表：[根、左子树、右子树]；
中序列表：[左子树、根、右子树]；

创建一个新节点，其值为当前找到的 根节点，左子树 和 右子树 递归等待答案；

然后递归，把 前序列表 和 中序列表 中的 左子树 提取出来，进一步拆分找到根、左、右；右子树同样操作。

这样，直到切分为长度为 3 的最小子树：

前序列表：[根、左、右]；
中序列表：[左、根、右]；

开始逐层返回，得到一整个树。

假定：
- 先序遍历：[3，_, _, _, _, _];
- 中序遍历：[0, 1, 2, 3, 4, 5];

那么我们就可以确定：根、左子树、右子树了:
- 先序遍历：['根', 左, 左, 左 , 右, 右]
- 中序遍历：[ 左 , 左, 左,'根', 右, 右]

然后求出：根的下标、左子树的长度
最后可以确定左子树、右子树的头尾两个下标了（见下文）

3. 抽象

假定：

前序列表的左子树，下标为：[preL, preR]
中序列表的左子树，下标为：[inL, inR]

// 根的值：
const rootValue = preorder[preL];
// 中序列表中，根坐标：
const index = inorder.indexOf(root);
// 由此找到左子树的长度
const subLen = index - inL;
// 前序列中的左子树、右子树
const preLeftTree = [preL + 1, preL + subLen];
const preRightTree = [preL + subLen + 1, preR];
// 中序列中的左子树、右子树
const inLeftTree = [inL, index - 1];
const inRightTree = [index + 1, inR];

4. 边界

每次递归，都是先确定一个根结点，然后以这个根结点为子树的基，构造左子树和右子树。

左右子树全部确定完成后，再返回这个 子树本身。

考虑：

面对某一个子序列，我们会先找根结点，再通过根结点下表找左子树和右子树的结点。

当某个子序列拆分的足够小：

长度为 3 和 3 以上时，一定有根结点，左子树和右子树可能有一个子树不存在；
长度为 2 时，一定有根结点，左子树和右子树必定有一个子树不存在；
长度为 1 时，一定有根结点，左子树和右子树 全部不存在；

综上，长度为 1 以上时，肯定有根结点，所以一定能创建一个子节点，不是问题的边界。

长度为 0 时，根结点、左子树、右子树都不存在，这个节点也不存在了。

找到了边界，当这个节点不存在，则遍历到了分支的边界，不会再返回新的结点了。

所以，边界就是当子序列的左下标 > 右下标时，证明这个序列已经不存在了，返回 null

if (preL > preR) {
  return null;
}

5. 求解

var buildTree = function(preorder, inorder) {
  const len = preorder.length
  // 开始递归
  return build(0, len-1, 0, len-1);

  function build(preL, preR, inL, inR) {
    // 边界，递归的 return
    if (preL > preR) {
      return null;
    }

    // 新建根结点
    const root = new TreeNode();
    root.val = preorder[preL];
    // 找根结点在中序列中的下标
    const index = inorder.indexOf(root.val);
    // 找到左子树的长度
    const subLen = index - inL;
    // 递归：左子树、右子树
    root.left = build(preL+1, preL+subLen, inL, index-1);
    root.right = build(preL+subLen+1, preR, index+1, inR);
    return root;
  }
};

106. 从中序与后序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树
0420，mid
动态规划，二叉树构造

思路同 105。

var buildTree = function(inorder, postorder) {
  // 特例
  if (!inorder || !postorder || inorder.length === 0 || postorder.length === 0)  return null;
  const len = inorder.length;
  return build(0, len-1, 0, len-1);

  function build(inL, inR, poL, poR) {
    // 边界
    if (inL > inR) {
      return null;
    }

    // 结点
    const root = new TreeNode();
    root.val = postorder[poR];
    // 下标
    const index = inorder.indexOf(root.val);
    const length = index - inL;
    // 递归左子树、右子树
    root.left = build(inL, index-1, poL, poL+length-1);
    root.right = build(index+1, inR, poL+length, poR-1);

    return root;
  }
};

相关题目：0511｜449. 序列化和反序列化二叉搜索树

107. 二叉树的层序遍历 II

107. 二叉树的层序遍历 II
0420, mid
二叉树构造

题解：

主要是对 curRes 放入 res 时的改动，只需要从之前的队头 push，改为队尾的 unshift 就可以了。

var levelOrderBottom = function (root) {
  if (!root) return [];
  const res = [];
  const quene = [];
  quene.push(root);

  while (quene.length) {
    // 记录层级信息
    const len = quene.length;
    const curRes = [];
    for (let i = 0; i < len; i++) {
      const node = quene.shift();
      curRes.push(node.val);
      
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    res.unshift(curRes);
  }
  return res;
};

102. 二叉树的层序遍历

102. 二叉树的层序遍历
0421， mid，quick
层序遍历基本功

var levelOrder = function(root) {
  // 特值
  if (!root) return [];
  // 队列
  //   unshift, [push]
  //   [shift], pop
  const quene = [];
  const res = [];

  // 先放入一根结点，然后while循环
  quene.push(root);
  while (quene.length){
    // 记录每层的长度、结果
    const levelLength = quene.length;
    const levelRes = [];
    // for遍历该行
    for (let i = 0; i < levelLength; i++){
      const node = quene.shift();
      levelRes.push(node.val);
      //❗️千万记得要判断存在，然后再push
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    res.push(levelRes);
  }
  return res;
};

103. 二叉树的锯齿形层序遍历

103. 二叉树的锯齿形层序遍历
0421，mid，answer
解析：https://leetcode-cn.com/problems/binary-tree-zigzag-level-order-traversal/solution/er-cha-shu-de-ju-chi-xing-ceng-xu-bian-l-qsun/
根据图表自己画一下就记忆深刻。

var zigzagLevelOrder = function (root) {
  // 特
  if (!root) return [];

  const res = []
  const quene = [];
  // true is ==>
  let flag = false;
  // shift, push
  quene.push(root);

  while (quene.length) {
    const levelLen = quene.length;
    const levelRes = []
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      // 在每层推入数时，需要根据flag进行正向/反向推入
      flag ? levelRes.unshift(node.val) : levelRes.push(node.val);
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);

    }
    flag = !flag;
    res.push(levelRes);
  }
  return res
};

199. 二叉树的右视图

199. 二叉树的右视图
0422，mid，quick
基本题，广度优先（层序遍历），深度优先（❓❓遍历）

解题一：广度优先

基于层序遍历，只需要在 level 每层返回该层遍历出的所有值的时候，只返回遍历到的最后一个值即可。

var rightSideView = function (root) {
  // 先层序，
  // 后只提取每层最右边的节点

  // 特
  if (!root) return [];

  //  shift<=======< push
  const res = [];
  const quene = [root];

  while (quene.length) {
    const levelLen = quene.length;
    const levelRes = []
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      levelRes.push(node.val);
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    // ❗️只返回该层的最后一个值。
    res.push(levelRes[levelRes.length - 1])
  }
  return res
};

更妙的解法：

不需要在 for 循环遍历每层结点的时候，用 levelRes 保存全部的结点值：

我们要的是 level 这一层中，最后一个节点的值。
levelLen 记录了该层的全部节点数
- 我可以在每遍历该层一个节点的时候，就让 levelLen 减1，当 levelLen 减少到 1 的时候，说明已经便利到最后一个节点了，然后记录这个节点的值即可。

// 仅贴出 while 内的代码
while (quene.length) {
  let levelLen = quene.length;
  while (levelLen) {
    const node = quene.shift();
    if (levelLen === 1) res.push(node.val);
    node.left && quene.push(node.left);
    node.right && quene.push(node.right);
    levelLen--;
  }
}

// 这样也可以，只需要判断 'i === levelLen - 1' 即可
while (quene.length) {
  const levelLen = quene.length;
  for (let i = 0; i < levelLen; i++) {
    const node = quene.shift();
    if (i === levelLen - 1) res.push(node.val)
    node.left && quene.push(node.left);
    node.right && quene.push(node.right);
  }
}

解法二：深度优先

https://leetcode-cn.com/problems/binary-tree-right-side-view/solution/shen-du-you-xian-sou-suo-by-shetia-2/

技巧：

深度优先，顺序是：根、右、左。
因为每一层只要一个数，所以用结果数组 res.length 来表示当前已经遍历过的深度，假如 res.length 值为 2，表示头两层已经遍历过，拿到了最右侧的值，所以接下来如果有对第二层的其他节点进行遍历，就跳过。
用 step 记录每次 dfs 时的深度。

var rightSideView = function (root) {
  // dfs
  if (!root) return [];
  const res = [];
  
  dfs(root, 0);
  
  // params: 当前结点、结点所在层数
  function dfs(node, level) {
    // 边界
    if(!node) return;

    // 层数相同就push
    if (level === res.length) {
      res.push(node.val);      
    }
    // 递归
    dfs(node.right, level + 1);
    dfs(node.left, level + 1);
  }
  return res;
};

637. 二叉树的层平均值

637. 二叉树的层平均值
0423, easy, quick
广度优先

求平均值用到了 reduce 要熟悉 reduce 的语法：

prev 是上一次 callback 的返回值。
最终返回 prev

// 有 initialValue
// 从 0 开始遍历，多循环一次。
// 循环第一次 preV 的值是 initV；
//          curV 的值是 Array[0]，
//          item 的值是 0
Array.reduce((preV, curV, item) => {
  return preV + curV
}, initV);

// 没有 initialValue
// 从 1开始遍历，
// 循环第一次 preV 的值是 Array[0]；
//          curV 的值是 Array[1]；
//                  item 的值是 1；

解法一：广度优先

var averageOfLevels = function (root) {
  // 层序遍历
  if (!root) return [];

  const quene = [root];
  const res = [];

  while(quene.length) {
    const levelVal = [];
    const levelLen = quene.length;
    for (let i = 0; i < levelLen; i++) {
      // shift <=========< push
      const node = quene.shift();
      levelVal.push(node.val);
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    // 求平均值
    const total = levelVal.reduce((acc, cur) => acc + cur, 0);
    const average = levelVal.length;
    res.push(total/average);
  }

  return res;
};

时间复杂度：每个数组遍历一边，O(n)
空间复杂度：
- quene、res： O(1)；
- levelVal、levelLen：O(n)；
- 总体空间复杂度依赖于树的深度，为 O(n)；

解法二：深度优先

我的思路是实现了一个用「深度优先」，遍历出一个「广度优先」；
levelVal 是一个二位数组，其成员是一个带层级的广度优先序列结果。
- 如一个数是：[3, 9, 20, 15, 7]，levelVal 值是 [[3], [9, 20], [15, 7]]

  // DFS
var averageOfLevels = function (root) {
  if (!root) return [];

  const res = [];
  // 二位数组：<node.val[]>[]，该数组的成员是每一层的结点值。
  // 也就是一个广度优先遍历出的结果
  const levelVal = [];
  dfs(root, 0)

  function dfs(node, level) {
    // 边界
    if (!node) return;

    // 数组长度 > 层数，已经定义过该层，可以直接push；反之没定义过，先定义再push
    // 最开始是第0层，levelVal.length = 1；
    levelVal.length > level ? levelVal[level].push(node.val) : levelVal.push([node.val]);

    dfs(node.left, level + 1);
    dfs(node.right, level + 1);
  }

  // 求每层的平均值
  levelVal.forEach(item => {
    const average = item.reduce((acc, cur) => acc + cur, 0) / item.length;
    res.push(average);
  })
  return res;
};

事实上没必要记录每一层的所有结点值，而只需要对值进行累加即可，这样之维护两个一维数组：
- levelTotal: 每层结点的值的总数 total
- levelCount：每层结点的个数 count

var averageOfLevels = function (root) {
  // DFS
  if (!root) return [];

  const res = [];
  const levelTotal = [];
  const levelCount = [];

  dfs(root, 0)

  function dfs(node, level) {
    // 边界
    if (!node) return;

    // 最开始是第0层，levelTotal.length = 1；
    // 第i层时，levelTotla.length = i+1
    levelTotal[level] ? levelTotal[level] += node.val : levelTotal[level] = node.val;
    levelCount[level] ? levelCount[level] += 1 : levelCount[level] = 1;

    dfs(node.left, level + 1);
    dfs(node.right, level + 1);
  }

  // 求每层的平均值
  levelTotal.forEach((item, index) => {
    res.push(item / levelCount[index]);
  })

  return res;
};

时间复杂度：所有节点只遍历一边，O(n)。
空间复杂度：只维护 3 个数组， O(1)。

429. N 叉树的层序遍历

429. N 叉树的层序遍历
0423, mid, quick
层序遍历

var levelOrder = function(root) {
  // bfs
  if (!root) return [];

  const quene = [root];
  const res = [];

  while(quene.length) {
    const levelLen = quene.length;
    const levelRes = [];
    for (let i = 0; i < levelLen; i++) {
      // shift <=====< push
      const node = quene.shift();
      levelRes.push(node.val);

      // 遍历n叉子节点
      if (node.children) {
        node.children.forEach( item => {
          quene.push(item);
        })
      }
    }
    res.push(levelRes);
  }
  return res;
};

515. 在每个树行中找最大值

515. 在每个树行中找最大值
0423，mid，quick
和 637 找平均数一样，bfs、dfs 都可以实现

BFS

var largestValues = function (root) {
  // bfs
  if (!root) return [];

  const quene = [root];
  const res = [];

  while (quene.length) {
    let levelRes = -Infinity;
    const levelLen = quene.length;
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      levelRes = Math.max(levelRes, node.val);
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    res.push(levelRes);
  }
  return res;
};

DFS

注意两点：

res 保存了每层的最大值；
在初始化判断 res[level] 是否存在时，不能用 res[level] 判断，必须用 res[level] !== undefined ，因为当 res[level] 的值为 0 时，也会判断为 不存在，返回 false；

var largestValues = function (root) {
  // dfs
  if (!root) return [];

  const res = [];
  dfs(root, 0);

  // 当前节点，深度
  function dfs(node, level) {
    // 边界
    if (!node) return;
    // 第 1 层时，level = 0, res.length = 1;
    // 第 n 层时，level = n-1, res.length = n;
    // 初始化
    if (res[level] !== undefined) {
      res[level] = Math.max(res[level], node.val);
    } else {
      res[level] = node.val
    }
    // 或者这样：
    // res[level] = res[level] === undefined ? node.val : Math.max(res[level], node.val);

    dfs(node.left, level + 1);
    dfs(node.right, level + 1);
  }
  return res;
};

116. 填充每个节点的下一个右侧节点指针

116. 填充每个节点的下一个右侧节点指针
0423，mid，quick answer
广度优先遍历

问题：

这道题刚开始干扰我的是返回值，其不是一个数组，而是直接返回 整个树，即 根结点 root。
- 注意在最终 return，和刚开始的特殊值 return，都是返回 root。

var connect = function (root) {
  if (!root) return root;       // 注意这里是return rook，不是 return []

  // bfs
  const quene = [root];

  while (quene.length) {
    const levelLen = quene.length;
    // 记录上一个节点
    let lastNode = null;
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      // 如果上一个节点不存在（说明是每层开头第一个），则不执行 next 赋值
      if (lastNode) {
        lastNode.next = node;
      }
      lastNode = node;
            // 递归
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
    // 对最后一个结点.next赋值为null
    lastNode.next = null;
  }

  return root;
};

117. 填充每个节点的下一个右侧节点指针 II

117. 填充每个节点的下一个右侧节点指针 II
0424，mid，quick
BFS
同上一道题 116 完全一样，只是写的更精炼了：

// BFS
var connect = function(root) {
  if (!root) return root;

  const quene  = [root];
  while (quene.length) {
    const len = quene.length;
    let lastNode = null;
    for (let i = 0; i < len; i++) {
      const node = quene.shift();
      if (i !== 0) lastNode.next = node;
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
      lastNode = node;
    }
    lastNode.next = null;
  }
  return root;
};

优化：内存优化

用三个指针省去队列的维护

核心：

第i层：已经通过 .next 建立联系，形成一个链表；
第i+1层：通过 .left 和 .right 与上层链表建立联系，利用上层链表，把 i+1 层也通过 .next 关联起来。

变量：

start：第i层链表的开始结点； nextStart：下一个链表的开始结点（也就是第i+1层的第一个结点）； lastNode：执行遍历时，第i+1层子节点的上一个结点

注意点：

每一个变量都有生命周期：定义、每次循环的初始化、每次循环结束的重置。

var connect = function(root) {
  if (!root) return root;
  // 变量：第i层链表的开始结点；下一个链表的开始结点（也就是第i+1层的第一个结点）；执行遍历时，第i+1层子节点的上一个结点
  // 根结点是第一个链表
  let start = root;
  let nextStart = null;
  let lastNode = null;

  while(start !== null) {
    // 遍历第i层链表
    for (let node = start; node !== null; node = node.next) {
      // 把子节点（i+1层）都关联起来
      node.left && connectNextPoint(node.left);
      node.right && connectNextPoint(node.right);
    }

    // 重置变量：确定下一轮链表的开头
    start = nextStart;
    nextStart = null;
    lastNode = null;
  }

  function connectNextPoint(node){
    // 绑定nextStart
    if(nextStart === null) nextStart = node;
    // 与lastNode链接
    if(lastNode !== null) lastNode.next = node;
    lastNode = node;
  }

  return root;
};

104. 二叉树的最大深度

104. 二叉树的最大深度
0424，easy，answer

方法一：深度优先

自己构造复杂了，直接递归 maxDepth 自身就可以。因为 maxDepth 的返回值既是我们要定义的递归函数的值，又是最终的返回值。所以就把 maxDepth 直接改造成递归函数就可以。不需要再 maxDepth 中单独定义一个递归函数。

var maxDepth = function (root) {
  if (!root) return root;

  // 递归：获得左子树最大深度
  const leftLevel = maxDepth(root.left);
  // 递归：获得右子树最大深度
  const rightLevel = maxDepth(root.right);
  // 返回：本结点最大深度 = 子树最大深度 + 1
  return Math.max(leftLevel, rightLevel) + 1;
};

自己最初的方法：

在 maxDepth 又定义了一个 dfs。

var maxDepth = function (root) {
  // dfs
  if (!root) return root;

  let maxLevel = 1;
  dfs(root, maxLevel);
  return maxLevel;

  function dfs(node, level) {
    if (node === null) return null;
    maxLevel = Math.max(maxLevel, level);
    dfs(node.left, level + 1);
    dfs(node.right, level + 1);
  }
};

方法二：广度优先

用 deep 表示遍历的层数，bfs 的特点是：

每当 while 循环一次，则遍历层数加深一次；
每当 for 循环一次，则便利同一层的一个节点；

var maxDepth = function (root) {
  if (!root) return root;

  const quene = [root];
  let deep = 0;

  while(quene.length) {
    const levelLen = quene.length;
    deep += 1;
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
  }
  return deep;
};

111. 二叉树的最小深度

111. 二叉树的最小深度
0424，easy，quick

方法一：广度优先 bfs

牢记：

while 循环是层级的，每一次 while 循环都是对一层的访问；
for 循环是结点级的，每一次 for 循环是对一个节点的访问；

本题要找最小深度：“深度” 就是 tree 中，从 根结点 到任意一个 叶子结点 的层级数。最小深度就是这些深度中最小的一个。

所以：

在 while 记录 “深度” 数据；
在 for 检测是否访问到叶子结点，一旦访问到（没有左右子树），就找到了最小深度。

var minDepth = function(root) {
  // bfs
  if (!root) return root;

  const quene = [root];
  let level = 0;

  while(quene.length) {
    const levelLen = quene.length;
    level += 1;
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      if (!node.left && !node.right) return level;
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
  }
};

方法二：深度优先 dfs

需要注意几点：

如果当前结点是叶子结点，则访问到了一个深度，返回层级 1；
如果当前节点不是一个叶子结点：
1. 一个子树存在，另一个子树不存在（为 null）。则该层节点的层数，只能取存在的子树的那个值。
  - 联想 root = [2,null,3,null,4,null,5,null,6] 的情况。
  - 所以，把子树不存在的深度值去值为无穷大，最终返回的就是另一个存在深度的子树值了。
2. 两个子树都存在，则返回这两个子树深度值的更小的那一个。

var minDepth = function (root) {
    // 当前节点不存在，返回 null
  if (!root) return null;
  // 叶子结点
  if (!root.left && !root.right) return 1;

  const leftDepth = minDepth(root.left) ?? Infinity;
  const rightDepth = minDepth(root.right) ?? Infinity;


  return Math.min(leftDepth, rightDepth) + 1;
};

226. 翻转二叉树

226. 翻转二叉树
0424，easy，quick
考点：递归+迭代两种方法都要会。

深度优先递归的思考方式，是从叶子结点开始翻转，逐层最后根结点进行翻转；

广度优先迭代的思考方式，是从根结点开始翻转，逐层最后叶子结点进行翻转；

总结：

深度优先、递归，做题的思考方式是自下而上的；
广度优先，迭代，做题的思考方式是自上而下的；

方法一：dfs 递归

每个结点都有两个动作：
- 左、右子树交换位置；
- 左、右子树各自反转其子树；
- 返回该节点。
注意递归边界，当遍历到叶子，则返回 null；

var invertTree = function (root) {
  if(!root) return null;
  const tempNode = root.left;
  root.left = invertTree(root.right);
  root.right = invertTree(tempNode);
  return root;
};

方法二：bfs 迭代

如果没有 for，只有 while。则每一次 while 循环都是一个结点。

var invertTree = function (root) {
  // bfs
  if(!root) return root;

  const quene = [root];
  while (quene.length) {
    const node = quene.shift();
    // exchange
    [node.left, node.right] = [node.right, node.left];
    node.left && quene.push(node.left);
    node.right && quene.push(node.right);
  }
  return root
};

144. 二叉树的前序遍历

144. 二叉树的前序遍历
0425，easy，quick
三种方法：递归、迭代、通用迭代

方法一：递归

var preorderTraversal = function(root) {
  if (!root) return [];

  const res = [];
  dfs(root)
  return res;

  function dfs(node){
    if (!node) return null;
    // 根、左、右
    res.push(node.val);
    dfs(node.left)
    dfs(node.right)
    return null
  }
};

方法二：迭代

栈结构直接解决

var preorderTraversal = function(root) {
  if (!root) return [];

  const stack = [root];
  const res = [];
  while (stack.length) {
    // 中
    const node = stack.pop();
    res.push(node.val);
    // 右
    node.right && stack.push(node.right);
    // 左
    node.left && stack.push(node.left);
  }
  return res;
};

方法三：通用迭代

对结点的遍历分为：

访问：左子树、本节点 + null、右子树；
读取：在 null 后的结点，读取其值；

每次访问到一个结点，按照遍历顺序对左子树、结点本身(值)、右子树进行访问（stack.push）。

但注意的是，访问值的时候，再额外 push 一个 null 标明下次要读取其值。

var preorderTraversal = function (root) {
  if (!root) return [];
  const stack = [root];
  const res = [];

  stack.push();
  
  while (stack.length) {
    // 每次循环拿出栈中的一个结点
    const point = stack.pop();
    if (point === null) {
      // 如果是 null，则要读取栈中下一个结点
      res.push(stack.pop().val);
    } else {
      // 如果不是 null，则访问这个节点：left/right/val，依次 push；
      point.right && stack.push(point.right); // 右
      point.left && stack.push(point.left);   // 左
      stack.push(point);    // 根
      stack.push(null);         // 根的尾巴
    }
  }
  return res
}

145. 二叉树的后序遍历

145. 二叉树的后序遍历
0425, easy, quick
三种方法：递归、迭代、统一迭代

方法一：递归

var postorderTraversal = function(root) {
  const res = []
  if (!root) return res;
  dfs(root);

  function dfs(node){
    node.left && dfs(node.left);  // 左
    node.right && dfs(node.right); // 右
    res.push(node.val); // 根
  }
  return res;
};

方法二：迭代

var postorderTraversal = function(root) {
  const res = [];
  if (!root) return res;
  const stack = [root];
  
  while(stack.length) {
    const node = stack.pop();
    res.push(node.val);     // 根
    node.left && stack.push(node.left);  // 左
    node.right && stack.push(node.right); // 右
  }
  // 翻转结果
  return res.reverse();
};

方式三：统一迭代

var postorderTraversal = function (root) {
  if (!root) return [];
  const res = [];
  const stack = [root];

  while (stack.length) {
    const point = stack.pop();
    if (point === null) {
      res.push(stack.pop().val);
    } else {
      // 根(null)、右、左      
      stack.push(point);
      stack.push(null);
      point.right && stack.push(point.right);
      point.left && stack.push(point.left);
    }
  }
  return res;
};

94. 二叉树的中序遍历

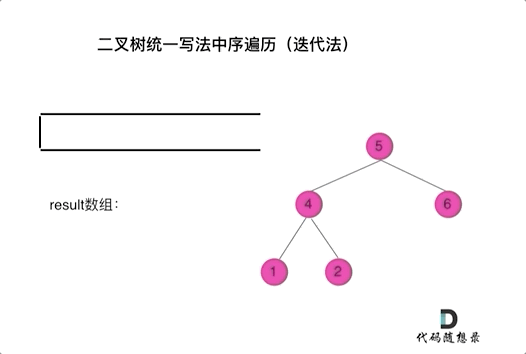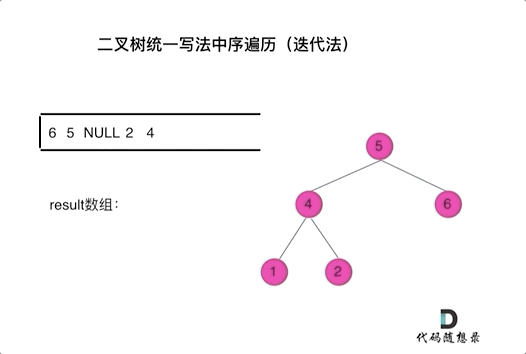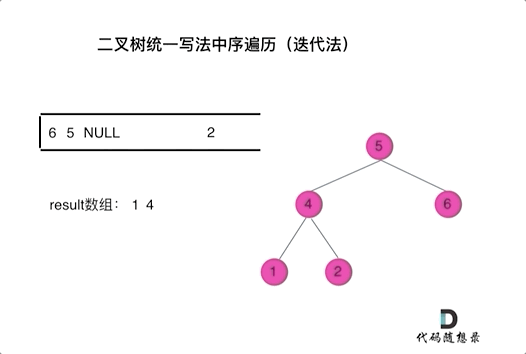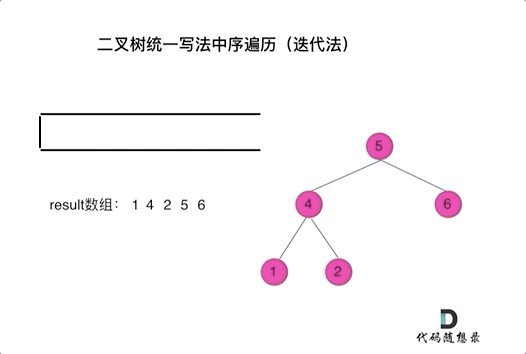
94. 二叉树的中序遍历
0425，easy，answer
常规迭代的解法二不好理解，要多看看

参考：二叉树的统一迭代法.md

中序遍历-迭代

中序遍历

方法一：递归

略，见 144. / 145. 题。

方法二：迭代

用 point 指向要取值的结点，栈结构来维护要遍历 左子树 结点；

一直往栈中压入左子树，一旦遇到叶子结点，则证明该分支已经到头；
- 判断是否为叶子结点的依据：当 point 指向了 null，则说明遍历已经到头了。
此时读取叶子结点的值，然后往栈中压入右子树；

var inorderTraversal = function (root) {
  if (!root) return [];
  const res = [];
  const stack = [];  // stack 不预先放入root，stack未来只会放入.left的结点
  let point = root;

  while (stack.length || point) {
    if (point !== null) {
      // 遍历左子树
      stack.push(point);    // 这里push(point)，不是push(cur.point)
      point = point.left;

    } else {
      point = stack.pop()
      res.push(point.val);
      point = point.right
    }
  }
  return res;
};

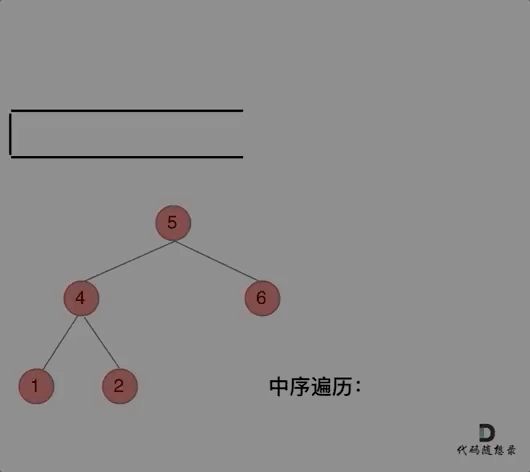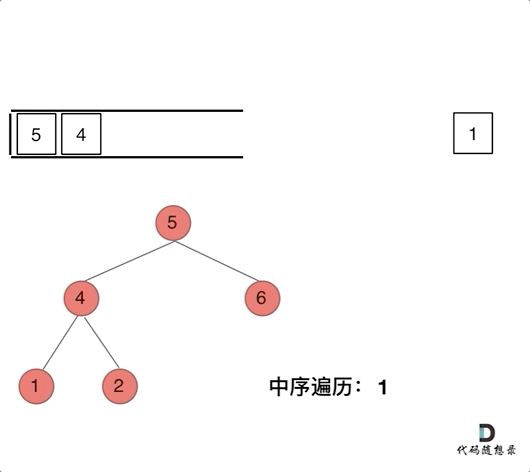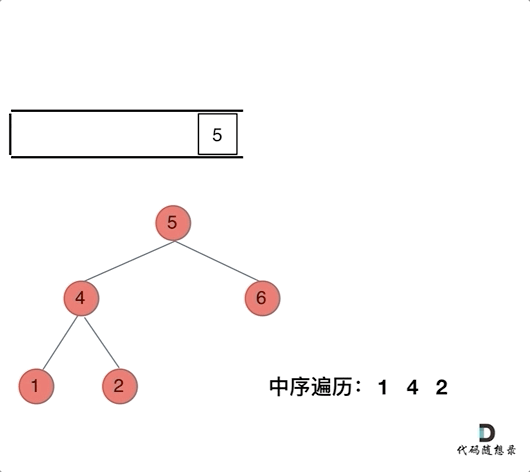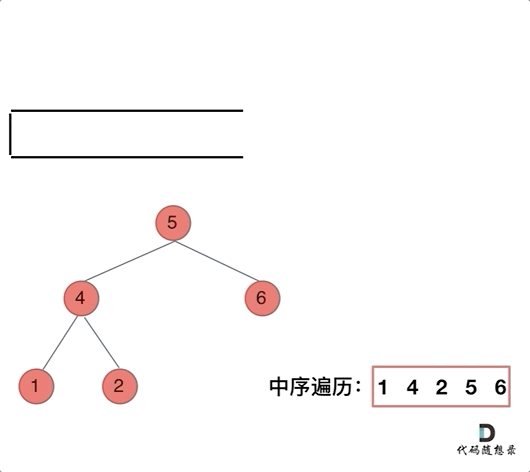
方法三：统一迭代

var inorderTraversal = function (root) {
  if (!root) return [];
  const res = [];
  const stack = [root];

  while (stack.length) {
    const point = stack.pop();
    // 取值
    if (point === null) {
      res.push(stack.pop().val);
      continue;
    }
    // 访问
    point.right && stack.push(point.right);
    stack.push(point);
    stack.push(null);
    point.left && stack.push(point.left);
  }
  return res;
};

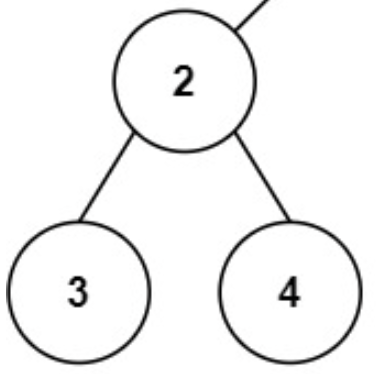
101. 对称二叉树

101. 对称二叉树
0425，easy，answer
对称二叉树 ---> 平衡二叉树

对称二叉树的最小判断结点，不是一个结点树为 3 的最小树：

而是一个结点数为 7 的树：

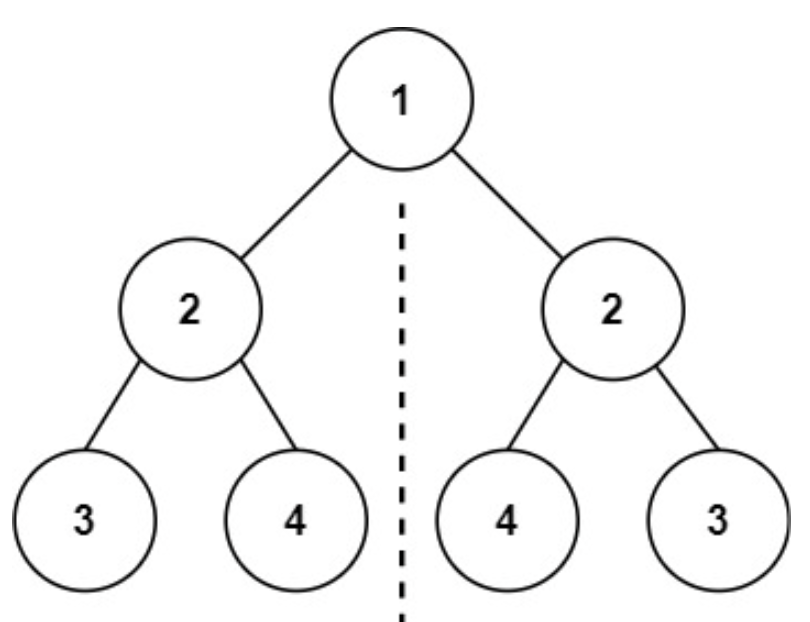
只有判断第三层 [3, 4, 4, 3] 对称，才可以决定该结点是否对称。

边界问题：

以 root 为判断的根，需要满足以下几点才可以决定平衡：

存在。root 的左右子节点存在性， root.left，root.right （对应图中的 2）；
1. root 的左右子节点都不存在，则该 root 为叶子结点，平衡；
2. root 的左右子节点有一个不存在，另一个存在，不平衡；
两个值相等。root 的左右子节点的值 root.left.val，root.right.val （对应图中的 2）；
1. 值相等，则平衡；不相等，则不平衡；
四个子树平衡。root 的左右子节点的子树： root.left.left、root.left.right、root.right.left、root.right.right；
1. inSide 内侧递归判断是否平衡；
2. outSide 外侧递归判断是否平衡；

方法一：递归

var isSymmetric = function (root) {
  if (!root) return false;
  // 递归 dfs
  // 判断是否平衡
  return compare(root.left, root.right);
  
  function compare(leftNode, rightNode) {
    // 边界问题
    // 叶子结点，到头了，没有子节点，所以返回 true
    if (leftNode === null && rightNode === null) return true;
    // 有一边空，另一边不空，肯定不平衡
    if ((leftNode === null && rightNode !== null) || (leftNode !== null && rightNode === null)) return false;

    // 判断这两个结点是否平衡；
    if (leftNode.val !== rightNode.val) return false;
    // 递归：判断子树是否平衡：
    // 内侧：左结点的右子树、右结点的左子树
    // 外侧：左结点的左子树、右结点的右子树
    const inSide = compare(leftNode.right, rightNode.left);
    const outSide = compare(leftNode.left, rightNode.right);
    return inSide && outSide;
  }
};

方法二：栈迭代

因为递归就是利用了函数的调用栈，所以我们自己维护一个 “调用栈”，就把递归改造成了迭代。
都是一次拿出来两个，然后比较是否对称，所以队列和栈的效果是完全一样的。
- 注意：队列是先进先出，栈是后进先出。
  - 所以一次取两个结点的时候 (left, right)，顺序会不一样 (注释)，其他逻辑完全相同。

var isSymmetric = function (root) {
  if (!root) return false;
  const stack = [];
  stack.push(root.right);
  stack.push(root.left);

  while (stack.length) {
    // ⚠️ 注意和队列对比取出的顺序
    const rightNode = stack.pop();
    const leftNode = stack.pop();

    // 存在
    if (leftNode === null && rightNode === null) continue;
    if ((leftNode === null && rightNode !== null) || 
              (leftNode !== null && rightNode === null)) return false;
    // 两个值相等
    if (leftNode.val !== rightNode.val) return false;
        // “递归” 四个子树平衡
    stack.push(leftNode.right, rightNode.left);
    stack.push(leftNode.left, rightNode.right);
  }
  return true;
};

方法三：队列迭代

var isSymmetric = function (root) {
  if (!root) return false;
  const quene = [];
  quene.push(root.left);
  quene.push(root.right);

  while (quene.length) {
    // ⚠️ 注意和栈对比取出的顺序
    const left = quene.shift();
    const right = quene.shift();
    // 存在
    if (left === null && right === null) continue;
    if (left !== null && right === null || left === null && right !== null) return false;
    // 两个值相等
    if (left.val !== right.val) return false;
    // 四个子树平衡
    quene.push(left.left, right.right);
    quene.push(left.right, right.left);
  }
  return true;
};

559. N 叉树的最大深度

559. N 叉树的最大深度
0425，easy，quick
思路见：104. 二叉树的最大深度

方法一：bfs 迭代

var maxDepth = function(root) {
    if (!root) return root;
    const quene = [root];
    let depth = 0;

    while (quene.length) {
      const levelLen = quene.length;
      for (let i = 0; i < levelLen; i++) {
        const node = quene.shift();
        // 循环遍历n叉树
        if (node.children) {
          node.children.forEach(item => {
            quene.push(item);
          })
        }
      }
      depth += 1;
    }
    return depth;
};

方法二：dfs 递归

var maxDepth = function (root) {
  // dfs
  if (!root) return root;
  let maxDepth = 0;
  dfs(root, 1);

  function dfs(node, level) {
    maxDepth = Math.max(maxDepth, level);
    if (node.children) {
      node.children.forEach(item => dfs(item, level + 1));
    }
  }

  return maxDepth;
};

// 精简代码：
// 直接把 maxDepth 作为递归函数。每调用一次，depth+1
var maxDepth = function (root) {
  if (!root) return root;
  let depth = 0;

  if (root.children) {
    root.children.forEach(item => depth = Math.max(depth, maxDepth(item)));
  }
  return depth + 1;
};

方法三：dfs 迭代

递归转化为迭代，就是把对应的函数函数调用栈实现，在栈保存了用到的参数：node 和 level；

var maxDepth = function (root) {
  // dfs
  if (!root) return root;
  let maxDepth = 0;
  const stack = [{ node: root, level: 1 }];

  while (stack.length) {
    const {node, level} = stack.pop();
    maxDepth = Math.max(maxDepth, level);
    if (node.children) {
      node.children.forEach(item => stack.push({ node: item, level: level + 1 }));
    }
  }

  return maxDepth;
};

222. 完全二叉树的节点个数

222. 完全二叉树的节点个数
0425，mid，answer
方法二利用了题目特点，这种解题思路要学习一下

方法一：dfs

var countNodes = function(root) {
  return dfs(root);

  function dfs(node){
    if (!node) return 0;
    return dfs(node.left) + dfs(node.right) + 1;
  }
};

// 递归函数dfs：是下面这个版本的简化
function dfs(node){
  // 结点不存在，则返回 0
  if (!node) return 0;
  // 结点存在，返回做左子树和右子树结点总和 + 1
  const leftNum = dfs(node.left);
  const rightNum = dfs(node.right);
  return leftNum + rightNum + 1
}

时间复杂度：O(n)
空间复杂度：O(log n)，算上了递归系统栈占用的空间

方法二：利用完全二叉树特点

var countNodes = function(root) {
  // 叶子结点
  if (!root) return 0;
  // 如果是满二叉树：左子树的左子树的左子树... 和 右子树的右子树的右子树... 深度相等；
  let [leftDepth, rightDepth] = [0, 0];
  let [leftNode, rightNode] = [root.left, root.right];
  while (leftNode) {
    leftDepth++;
    leftNode = leftNode.left;
  }
  while (rightNode) {
    rightDepth++;
    rightNode = rightNode.right;
  }
  // 满二叉树： node总数 = 2^层数-1
  if (leftDepth === rightDepth) return (2 << leftDepth ) - 1
                                       // 不同写法：return (2 ** leftDepth )
  // 不是满二叉树：递归求各自子树的node总数
  return countNodes(root.left) + countNodes(root.right) + 1
};

计算满二叉树时，用到了位移运算，用 ** 2 ，也可以：

3 << 1 // 相当于：3 * 2 ** 1 = 6
3 << 4 // 相当于：3 * 2 ** 4 = 32
2 << 3 // 相当于：2 * 2 ** 3，相当于 2 ** 4，相当于 2^4

// 左移1位就是扩大2倍
// 左移2位就是扩大4倍

110. 平衡二叉树

110. 平衡二叉树
0425，easy，answer
平衡二叉树定义，后序遍历

一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1

某个结点的：

高度：从叶子结点到这个节点的最短路径；
深度：从根结点到这个节点的最短路径；

求高度，自底向上的遍历，所以采用后序遍历（左、右、根）

参考文章：平衡二叉树.md

var isBalanced = function(root) {
  // 递归
  return getNodeDepth(root) === -1 ? false : true;

  function getNodeDepth(node){
    //边界，遍历到边界，返回高度0
    if (!node) return 0;  
  
    //分别获得左、右子树的高度，如果返回了 -1 表明"子树"不是平衡树，本树也不是，直接返回 -1；
    let leftDepth = getNodeDepth(node.left);
    if (leftDepth === -1) return -1;
    let rightDepth = getNodeDepth(node.right);
    if (rightDepth === -1) return -1;
    
    //左右子树都是平衡树，计算它们的高度差，如果 <=1，则返回：更高的子树+1，否则返回 -1
    return Math.abs(leftDepth - rightDepth) > 1 
        ? -1 
            : Math.max(leftDepth, rightDepth) + 1;
  }
};

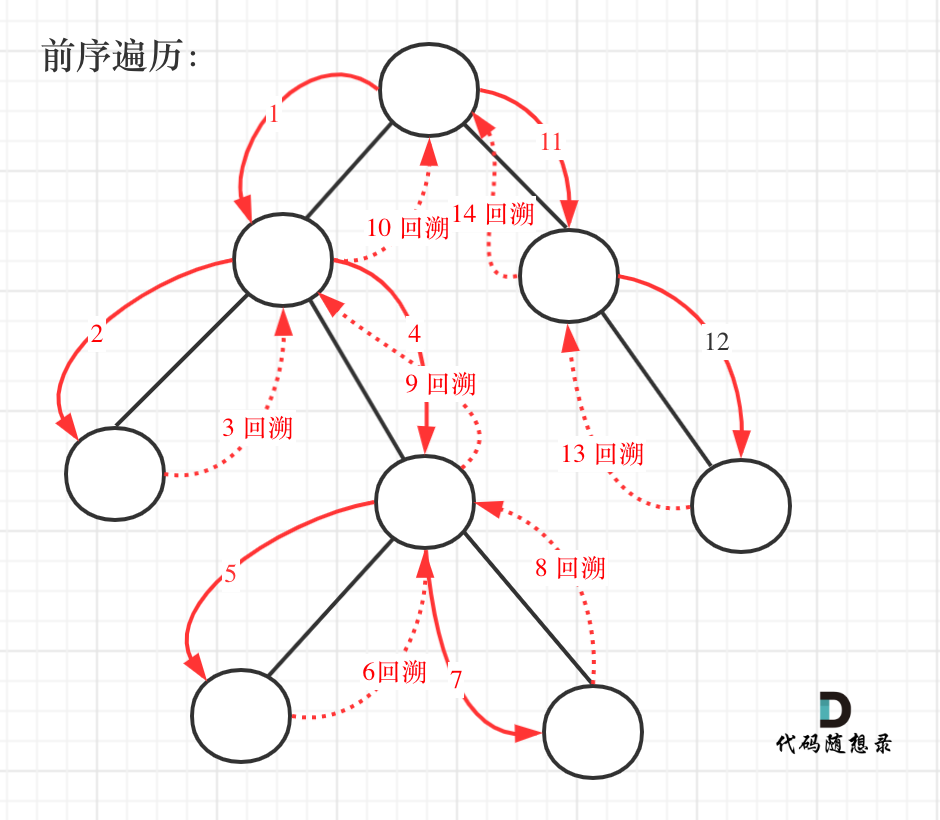
257. 二叉树的所有路径

257. 二叉树的所有路径
0426，easy，answer
先序遍历的迭代/递归

明白什么时候用：

先序遍历：在自顶向下的遍历中，需要获得遍历过的每一个结点的信息；
- 如：二叉树的所有路径，二叉树的最大深度等等；
后序遍历：在自顶向下的遍历中，获得最后一个结点的信息；
- 如：二叉树的全部叶子结点的高度，判断平衡二叉树等等；

方法一：递归+回溯

递归的函数：参数、返回值。
1. 参数：本次递归节点、本条路径 path、结果数组 result；
递归的返回条件。
1. 当递归到一个叶子结点时返回。此时把结果 push 到 result 中。
递归 + 回赎
1. 递归：当该节点不是叶子结点，存在左、右子树的时候，递归的向下探寻路径；
2. 回赎：当遍历到叶子结点，则结束该条路径遍历。向上回溯到父节点，遍历下一个子树的路径。

参考文章：二叉树的所以路径.md

var binaryTreePaths = function (root) {
  if (!root) return [];
  const result = []
  traversal(root, '', result)

  // 递归
  function traversal(node, path, result) {
    // 边界：叶子节点,path 写入 result
    if (node.left === null && node.right === null) {
      respath = (path + '->' + node.val).substr(2)
      result.push(respath);
    }
    //递归+回溯
    node.left && traversal(node.left, path + '->' + node.val, result);
    node.right && traversal(node.right, path + '->' + node.val, result);
  }
  return result;
};

substr 获得字符串的子串，参数1: 子串开头，参数2: 子串的长度；

方法二：迭代

用 stack 代替函数调用栈。

var binaryTreePaths = function (root) {
  if (!root) return [];
  // 迭代：用 stack 代替函数递归：保存 {node + path}
  const stack = [];
  const result = []

  stack.push({ node: root, path: '' });

  // 遍历
  while (stack.length) {
    const { node, path } = stack.pop();
    // 边界：叶子节点,path 写入 result
    if (node.left === null && node.right === null) {
      respath = (path + '->' + node.val).substr(2);
      result.push(respath);
    }
    //注意调用顺序，因为栈的特性，顺序与递归相反：
    node.right && stack.push({ node: node.right, path: path + '->' + node.val });
    node.left && stack.push({ node: node.left, path: path + '->' + node.val });
  }
  return result;
};

100. 相同的树

100. 相同的树
0426，easy，quick
和对称二叉树类似

方式一：递归 dfs

var isSameTree = function(p, q) {
  // 递归：先序遍历
  return compare(p, q)

  function compare(p, q){
    // 边界
    // 结点都不存在 / 有一个不存在
    if (p === null && q === null) return true;
    if (p === null || q === null) return false;
    
    // 结点值
    if (p.val !== q.val) return false;
    // 都是叶子结点
    if (p.left === null && p.right === null && q.left === null && q.right === null) return true;
    // 递归
    const left = compare(p.left, q.left);
    const right = compare(p.right, q.right);
    return left && right
  }
};

// 优化一下：
var isSameTree = function (p, q) {
  // 都是叶子结点
  if (p === null && q === null) return true;
  // 有一个不是叶子结点，有一个是叶子结点
  if (p === null || q === null) return false;
  // 值不相等
  if (p.val !== q.val) return false;
  // 递归：判断子树
  return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

// 还能优化：

方法二：迭代 bfs

也可以使用 dfs 迭代，就是换成了 stack 结构。
- 注意：在对递归进行改造时，要注意增加回溯逻辑：以往的 return true 全部改为 continue.
  - 这是因为，true 只判断了当前节点符合了相等逻辑，但其余节点尚未遍历，还不确定是否相等。所以要回溯到父节点，对其他分支进行遍历。
- 要把所有的分支都遍历并判断一遍。
- continue：本轮循环已经可以确定节点相等，所以不需要（也不能）执行后面的代码了。

var isSameTree = function (p, q) {
  // 用层序遍历（quene）和先序遍历（stack）迭代也可以
  if (!p && !q) return true;
  const quene = [{ leftNode: p, rightNode: q }];

  while (quene.length) {
    const { leftNode, rightNode } = quene.shift();
    // 边界
    // 结点都不存在 / 有一个不存在
    if (leftNode === null && rightNode === null) continue;  //注意，不是return true
    if (leftNode === null || rightNode === null) return false;

    // 结点值
    if (leftNode.val !== rightNode.val) return false;
    // 都是叶子结点
    if (
      leftNode.left === null && leftNode.right === null
      && rightNode.left === null && rightNode.right === null
    ) continue;  //注意，不是return true
    // 判断下一个结点是否相等
    quene.push({ leftNode: leftNode.left, rightNode: rightNode.left })
    quene.push({ leftNode: leftNode.right, rightNode: rightNode.right })
  }
  return true;
};

404. 左叶子之和
0426，easy，answer
左叶子定义需要明白

左叶子的定义：

如果左节点不为空，且左节点没有左右孩子，那么这个节点的左节点就是左叶子。

左叶子的判断：

如果该节点的左节点不为空，该节点的左节点的 左节点, 右节点均为空，则为一个左叶子。

方法一：递归 dfs

var sumOfLeftLeaves = function(root) {
  let res = 0;
  if (!root) return res;
  dfs(root);
  
  function dfs(node) {
    if (!node) return 
    // 如果该节点的左节点不为空，该节点的左节点的 `左节点, 右节点` 均为空，则为一个左叶子。
    if (node.left && !node.left.left && !node.left.right) {
      res += node.left.val;
    }
    node.left && dfs(node.left);
    node.right && dfs(node.right);
  }
  return res
};

方法二：迭代 bfs

迭代用 dfs 也可以，用 stack 结构，注意左右子节点 push 的顺序；

var sumOfLeftLeaves = function(root) {
  let res = 0;
  if (!root) return res;
  const quene = [root];

  while (quene.length) {
    const node = quene.shift();
    if (!node) continue;

    // 如果该节点的左节点不为空，该节点的左节点的 `左节点, 右节点` 均为空，则为一个左叶子。
    if (node.left && !node.left.left && !node.left.right) {
      res += node.left.val;
    }
    node.left && quene.push(node.left);
    node.right && quene.push(node.right);
  }
  return res
};

方法三：迭代 dfs

var sumOfLeftLeaves = function(root) {
  let res = 0;
  if (!root) return res;
  const stack = [root];

  while (stack.length) {
    const node = stack.pop();
    if (!node) continue;

    // 如果该节点的左节点不为空，该节点的左节点的 `左节点, 右节点` 均为空，则为一个左叶子。
    if (node.left && !node.left.left && !node.left.right) {
      res += node.left.val;
    }
    node.right && stack.push(node.right);  // 右：顺序颠倒
    node.left && stack.push(node.left);    // 左
  }
  return res
};

513. 找树左下角的值

513. 找树左下角的值
0426，mid，quick
递归 dfs 有点忘记了，见：104. 二叉树的最大深度

⚠️ 注意：if (i === 0) 我写成了 if (i = 0) 看了好久没发现，自己需要注意了，别粗心。

方法一：迭代 bfs

var findBottomLeftValue = function (root) {
  // bfs
  let res = NaN;
  if (!root) return res;
  const quene = [root];

  while (quene.length) {
    const levelLen = quene.length;
    for (let i = 0; i < levelLen; i++) {
      const node = quene.shift();
      if (i === 0) res = node.val;    // 判断中我写成了 `1 = 0`
      node.left && quene.push(node.left);
      node.right && quene.push(node.right);
    }
  }
  return res;
};

方法二：递归 dfs

找深度最深的子节点、前序遍历（确保是最左边的）

var findBottomLeftValue = function (root) {
  // dfs 深度
  if (!root) return 0;
  let resLevel = 0;
  let res = null;
  dfs(root, 1);

  function dfs(node, level) {
    // 叶子结点判断深度：
    if (!node.left && !node.right) {
      if (level > resLevel) {
        resLevel = level
        res = node.val;
      }
    }
    node.left && dfs(node.left, level + 1);
    node.right && dfs(node.right, level + 1);
  }
  return res;
};

112. 路径总和

112. 路径总和
0427，easy，quick

方式一：dfs 递归

涉及到回溯和及时返回，一旦找到满足条件的路径，就停止继续遍历，直接返回。
所以对递归要 有返回值。

var hasPathSum = function (root, targetSum) {
  if (!root) return false;
  // dfs，先序
  return dfs(root, 0);

  function dfs(node, lastSum) {
    const curSum = lastSum + node.val;
    // 叶子结点判断
    if (!node.left && !node.right) {
      return curSum === targetSum ? true : false;
    }
    if (node.left && dfs(node.left, curSum)) return true;
    if (node.right && dfs(node.right, curSum)) return true;
    return false;
  }
};

方式二：dfs 迭代

主要涉及到两个更改：
- 栈中保存：递归的两个参数；
- 递归的返回值，true 不变继续返回，false 调整为 continue

var hasPathSum = function (root, targetSum) {
  if (!root) return false;
  // dfs，先序
  const stack = [{ node: root, count: 0 }];

  while (stack.length) {
    const { node, count } = stack.pop();
    const curSum = count + node.val;
    // 叶子结点
    if (!node.left && !node.right) {
      if (curSum === targetSum) return true 
      continue;
    }
    node.right && stack.push({ node: node.right, count: curSum });
    node.left && stack.push({ node: node.left, count: curSum });
  }
  return false;
};

113. 路径总和 II

113. 路径总和 II
0427，mid，quick

方式一：dfs 递归

var pathSum = function (root, targetSum) {
  const res = [];
  if (!root) return res;
  // dfs
  dfs(root, 0, [])

  function dfs(node, count, path) {
    const curSum = count + node.val;
    const curPath = [...path];
    curPath.push(node.val);
    // 叶子结点
    if (!node.left && !node.right) {
      if (targetSum === curSum) res.push(curPath);
      return
    }
    node.left && dfs(node.left, curSum, curPath);
    node.right && dfs(node.right, curSum, curPath);
  }
  return res;
};

// 显式回溯，少一个 ...path 的复制操作，提升速度
var pathSum = function (root, targetSum) {
  const res = [];
  if (!root) return res;
  // dfs
  dfs(root, 0, []);
  return res;

  function dfs(node, count, path) {
    const curSum = count + node.val;
    path.push(node.val);
    // 叶子结点
    if (!node.left && !node.right) {
      if (targetSum === curSum) res.push([...path]);

    }
    node.left && dfs(node.left, curSum, path);
    node.right && dfs(node.right, curSum, path);
    path.pop();    // ❗️回溯
  }
};

方式二：bfs 迭代

回溯的解决方式，是把当前节点状态都在 quene 中保存：

当前节点的路径总数值：count；
当前节点的路径：path。注意 path 在保存时要浅拷贝一份。

var pathSum = function (root, targetSum) {
  const res = [];
  if (!root) return res;
  // bfs
  const quene = [{ node: root, count: 0, path: [] }];

  while (quene.length) {
    const { node, count, path } = quene.shift();
    const curCount = count + node.val;
    const curPath = [...path];
    curPath.push(node.val);
    // 叶子结点：
    if (!node.left && !node.right) {
      if (targetSum === curCount) res.push(curPath);
    }
    node.left && quene.push({ node: node.left, count: curCount, path: curPath });
    node.right && quene.push({ node: node.right, count: curCount, path: curPath });
  }
  return res;
};

方法三：dfs 迭代 + map 优化内存

用map存储节约内存

key为当前节点，value为父节点，
需要在定义后初始化放入 map.set(root, null)
当找到符合条件的根节点后，可通过 while 循环向上查找，即可找到完整的路径。

var pathSum = function (root, targetSum) {
    if (!root) return [];
    // dfs 迭代
    const res = [];
    const stack = [{ node: root, curSum: targetSum }];
    // 用map存储节约内存，key为当前节点，value为父节点，通过while循环向上查找，即可找到完整的路径。
    const map = new Map();
    // 初始化父节点指向null
    map.set(root, null);
    while (stack.length) {
        let { node, curSum } = stack.pop();
        curSum -= node.val;
        if (!node.left && !node.right && curSum === 0) {
            res.push(getPath(node));
        }
        if (node.right) {
            map.set(node.right, node);
            stack.push({ node: node.right, curSum });
        }
        if (node.left) {
            map.set(node.left, node);
            stack.push({ node: node.left, curSum });
        }
    }

    // while向上查找完整路径
    function getPath(node) {
        const res = [];
        while (node !== null) {
            res.unshift(node.val);
            node = map.get(node);
        }
        return res;
    }
    return res;
};

437. 路径总和 III

面试题 04.12. 求和路径

437. 路径总和 III
面试题 04.12. 求和路径
0427，0428，mid，hard answer
深度优先，求和

思路：

遍历每一个节点，然后记录从 root 到这个节点遍历过的所有值，用 path 记录。
- 每当遍历到一个新节点，就从这个节点为底，自下而上（从后往前）的读取 path 中的值，不断累加，找到所有累加值 === sum 的情况，每找到一个就让结果 res + 1；
两个重点：
- 求和路径中，有负值的节点、不一定是从根结点开始，不一定是从叶子结点开始的。
- 遍历是从上往下，而每遍历一个节点，是从下往上计算的。相当于把叶子结点当成了一个端点。
- 一个路径上可能有多个满足累加和 === sum 的情况，需要全部考虑在内。

方法一：自底向上求和（自己的方法）

var pathSum = function (root, targetSum) {
  let res = 0;
  if (!root) return res;
  dfs(root, []);
  return res;


  function dfs(node, path) {
    // 加一个子节点，计算当前的 path 值
    const curPath = [...path, node.val];
    let curSum = 0;
    // 从最后一个节点往前倒着遍历，计算满足的情况
    for (let i = curPath.length - 1; i >= 0; i--) {
      curSum += curPath[i];
      // 如果当前 path sum 相等，方法加1
      if (curSum === targetSum) res += 1;
    }

    node.left && dfs(node.left, curPath);
    node.right && dfs(node.right, curPath);
  }
};

时间复杂度：for 循环一个，递归一个：O(n^2)；

空间复杂度：维护数组 path，O(n^2)；

方法二：自顶向下求和

链接：https://leetcode-cn.com/problems/path-sum-iii/solution/lu-jing-zong-he-iii-by-leetcode-solution-z9td/

自底向上的缺点是每个节点都维护了一个 path 数组。
- 而把 sum 每次见去 val，省去了维护 path，而仅仅需要维护一个数字。
递归逻辑：
假设 root 到 A 结点的路径和为 targetSum，那么自然 root 下一个子结点到 A 结点的路径和为 targetSum - 1。

// dfs
// 以 root 为根结点，递归遍历二叉树的每个节点，对节点求rootSum，然后将每个节点所有求的值进行相加求和返回。
var pathSum = function (root, targetSum) {
  if (!root)  return 0;

    let ret = rootSum(root, targetSum);
    ret += pathSum(root.left, targetSum);
    ret += pathSum(root.right, targetSum);
    return ret;
  };

  // dfs，
  // 以 root 为根结点，向下遍历所有路径，返回满足路径和为 targetSum 的总数
  const rootSum = (root, targetSum) => {
    let ret = 0;
    if (root.val === targetSum) ret++;
    // 递归逻辑：
    // 假设root到A结点的路径和为targetSum，那么自然root下一个子结点到A结点的路径和为 targetSum - 1，
    ret += root.left ? rootSum(root.left, targetSum - root.val) : 0;
    ret += root.right ? rootSum(root.right, targetSum - root.val) : 0;
    return ret;
  }

pathSum 是递归二叉树的所有结点，让每个节点都调用一次 rootSum，然后累加 rootSum 的返回值；
rootSum 是以 root 为根结点，递归所有路径，求路径和满足 sum 的总数。

综上，时间复杂度：O(n^2)；空间复杂度：O(n)，递归需要在栈上开辟空间。

方法三：前缀和

参考：https://leetcode-cn.com/problems/path-sum-iii/solution/tong-ge-lai-shua-ti-la-qian-zhui-he-tu-j-trcq/

思考，为什么别人的解析看不懂？
- 自己没有去一步步落实，不能光看，要边看边画图，边手算。根据解析自己找一找规律，画出一个树状图。后面看懂了就是因为有一个解析它画了图，一目了然。
思考，方法一中哪些地方需要改进？
- 主要是每次 dfs 都保存了一个完整的路径 path，在计算路径和是否相等时，会用 for 循环计算一次，想办法把重复计算的 for 循环变成 O(1) 的复杂度。
- 解决：用一个 Map 记录每一次 dfs 时，计算的结果，这样结果就可以重复利用。
- 利用了前缀和的概念：
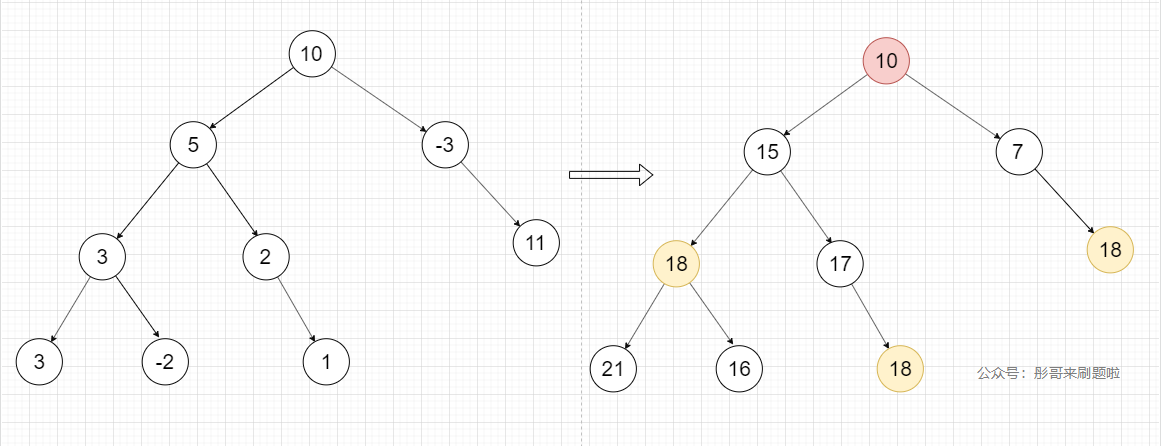
- 在 dfs 遍历每一个节点的时候，把节点到 root 的路径和做一个记录，用 Map 结构。
- 当 targetSum 为 6 时，可以看到左下角叶子结点 21 到它的祖父节点 15 的差，正好是 21 - 15 = 6，即找到了一个满足的路径。
- 所以，我们在用 Map 结构作记录时，仅保存路径上存在的路径和（key），和存在的次数（value）即可。然后当我们遍历到一个新节点，就用 TargetSum - 新节点路径和 在 Map 中查找。得到的 value 就是这新节点满足条件的路径总数。
- 需要注意：
  - 最开始先放入根结点 (0, 1) 到 Map 中；
  - 及时回溯，从 Map 中删除不要的数据；

var pathSum = function (root, targetSum) {
  let res = 0;
  if (root == null) return res;

  // 记录路径中某个前缀和出现的次数
  const count = new Map();
  // 防止包含根节点的时候找不到
  count.set(0, 1);
  dfs(root, 0);
  return res;

  // dfs：当前节点，map结构，上一次前缀和，目标总数
  function dfs(node, curSum) {
    if (!node) return null;

    // 判断是否存在符合条件的前缀和
    curSum += node.val;
    res += count.get(curSum - targetSum) || 0;
    // 将当前前缀和记录下来
    count.set(curSum, (count.get(curSum) || 0) + 1);

    // 继续往下递归
    dfs(node.left, curSum);
    dfs(node.right, curSum);

    // 回溯，恢复状态
    count.set(curSum, count.get(curSum) - 1);
  }
}

70. 爬楼梯

70. 爬楼梯
0428，easy，answer
动态规划，不能用dfs

方法一：[动态规划] 正解

dp[n] == dp[n-1] + dp[n-2];

var climbStairs = function (n) {
  if (n < 3) return n;
  // 
  const dp = [];
  dp[1] = 1;
  dp[2] = 2;

  for (let i = 3; i <= n; i++) {
    dp[i] = dp[i - 1] + dp[i - 2];
  }
  return dp[n];
};

时间复杂度：循环执行 n 次，时间复杂度为 O(n)。
空间复杂度：用一个长度为 n 的数组维护，空间复杂度为 O(n)。

方法二：优化-动态规划

转换公式中得出结论：第 n 个值只受 n-1 和 n-2 值的影响。所以没有必要维护一整个数组，只需要维护最后两个数即可。

var climbStairs = function (n) {
  if (n < 3) return n;
  // dp[n] == dp[n-1] + dp[n-2];
  let dp1 = 1;
  let dp2 = 2;

  for (let i = 3; i <= n; i++) {
    // dp[i] = dp[i - 1] + dp[i - 2];
    const temp = dp2;
    dp2 = dp2 + dp1;
    dp1 = temp;
  }
  return dp2;
};

时间复杂度：循环执行 n 次，时间复杂度为 O(n)。
空间复杂度：用 2 个数维护，空间复杂度为 O(1)。

方法三：[dfs] 超时

var climbStairs = function (n) {
  let res = 0;
  if (n === 0) return res;
  dfs(n);
  return res;

  // dfs:每次可以选择 1, 2
  function dfs(n) {
    if (n - 2 > 0) {
      dfs(n - 2);
    } else {
      if (n - 2 === 0) res += 1;
    }

    if (n - 1 > 0) {
      dfs(n - 1);
    } else {
      if (n - 1 === 0) res += 1;
    }
  }
};

时间复杂度：递归每一个节点，当传入数值为 n 时，递归执行了 n 次，时间复杂度为 O(n)。
- 但是递归时分为 1 和 2 两个情况，虽然不是 O(n^2)，但是也比动态规划多。

这里只用了常数个变量作为辅助空间，故渐进空间复杂度为 O(1)。

988. 从叶结点开始的最小字符串

988. 从叶结点开始的最小字符串
0428，mid，quick
dfs 的使用

方法一：dfs

注意审题：
- 最终的值是一个字符串，但节点值是数字，需要转换：String.fromCharCode(97 + node.val) 公式。
- 最终的值是倒序的，也就是说叶子结点在开头，根结点在结尾。

var smallestFromLeaf = function (root) {
  // 只返回一个即可
  // 返回一个从root到叶子的路径，要求值最小。

  // dfs
  let res = Infinity;
  if (!root) return '';
  dfs(root, '');
  return res;

  function dfs(node, lastVal) { 
    // String.fromCharCode(64 + 1);  --> A
    const valNumber = String.fromCharCode(97 + node.val);
    const val = '' + valNumber + lastVal;
    
    // 到达叶子节点，返回值
    if (!node.left && !node.right) { 
        if (res === Infinity) res = val;
      res = res > val ? val : res;
      return;
    }
    node.left && dfs(node.left, val);
    node.right && dfs(node.right, val);
  }
};

数字向字母的转化：

const valNumber = String.fromCharCode(97 + node.val);

543. 二叉树的直径

543. 二叉树的直径
0428，easy，answer
dfs

我一直在求从 root 到某个节点的最大深度，而不是从 “某个节点” 到叶子结点的最大深度。

所以要明确返回值，明确始端和末端的值。

为什么当时没想到？

没思路时，从末端开始倒退，当节点为 null，深度就是 0；当节点为叶子结点，深度就是1；
按照递归思路考虑问题：
- 递归的入参和返回值：
  - 入参：node 。
  - 出参：node 为基的最大深度。
  - 递归结束：当 node 不存在时，此时深度为 0；（叶子结点深度为 1）
- 递归内容：
  - 求分别递归求左子树和右子树的最大深度 maxDepth，然后本节点的最大深度就是 maxDepth + 1 这也是返回值。
明确两个问题：
- 求 node 结点为基的最长直径 === node.left 最大深度 + node.right 最大深度
- 求 node 结点为基的最大深度 === Math.max( node.left 最大深度, node.right 最大深度 )

var diameterOfBinaryTree = function (root) {
  if (!root) return 0;
  let max = 0;
  dfs(root);
  return max;

  // 求 node 的最大深度。
  function dfs(node) {
    if (!node) return 0;

    const left = dfs(node.left);
    const right = dfs(node.right);

    // 求 node 节点的直径 = node.left最大深度 + node.right最大深度
    // 比较并保存最大直径
    max = Math.max(max, left + right);

    // 返回：node 节点的最大深度 = node 子节点的最大深度 + 1；
    return Math.max(left + right) + 1;
  }
};

687. 最长同值路径

687. 最长同值路径
0428，mid，answer
区分：最长路径和深度的概念

最长路径：

只有一个节点时，最长路径 0，相同值 1
node有 2 个结点时，最长路径 = node.left + node.right，

相同值：

在判定最长路径时，要先设定左右子树的最长路径为 0。只有 node.val 与 node.left.val 相等，最长路径才是 dfs(node.left)，右子树同理；

var longestUnivaluePath = function (root) {
  if (!root) return 0;
  // 相同值的最长路径
  let max = 0;
  dfs(root);
  return max;

  // dfs返回值：node的最大深度
  function dfs(node) {
    if (!node) return 0;

    // 左子树和右子树的最大深度
    const left = dfs(node.left);
    const right = dfs(node.right);

    //  左子树和node值相同，才记录最大深度，否则左子树深度为0. 右子树同理
    let leftLength = 0;
    let rightLength = 0;
    if (node.left && node.val === node.left.val) {
      leftLength = left;
    }
    if (node.right && node.val === node.right.val) {
      rightLength = right;
    }

    // 相同值最长路径：
    max = Math.max(max, leftLength + rightLength);

    // node(相同值)的最大深度
    return Math.max(leftLength, rightLength) + 1;
  }
};

124. 二叉树中的最大路径和

124. 二叉树中的最大路径和
0428，hard，answer
本质上是 988、543 一脉相承的，但有了更好的题解思路：

树问题的本质：

所有树的题目，都想成一颗只有根、左节点、右节点的小树。然后一颗颗小树构成整棵大树，所以只需要考虑这颗小树即可。
接下来分情况，按照题意：一颗三个节点的小树的结果只可能有如下6种情况，然后一一去分析：
1. 根 + 左 + 右
2. 根 + 左
3. 根 + 右
4. 根
5. 左
6. 右

解题思路

二叉树 abc，a 是根结点（递归中的 root），bc、是左、右子结点（代表其递归后的最优解）。

    a
   / \
  b   c 

最大的路径，可能的路径情况：

b + a + c，以 a 结点为基的最大路径。
b + a + a 的父结点。以 a 的某一个父节点为最大路径，b + a 只是它其中一个分支的一小段；
c + a + a 的父结点。以 a 的某一个父节点为最大路径，c + a 只是它其中一个分支的一小段；

情况一：在我们每次遍历一个 node 时，通过 Math.max() 比较计算；

情况二、三：在我们遍历完 node 时提供的返回值，给 a 的父节点做参考。

负值的情况：

在计算 b 和 c 时，如果遇到结果为负数，那直接舍弃，分支的结果为 0；

和 988、543 不同的是，这里是求的不再是层数和深度，而是值的总和，所以返回值应当是 + node.val。

var maxPathSum = function(root) {
  if (!root) return 0
  let max = -Infinity;
  dfs(root);
  return max;

  // 返回 node 节点大单边最大路径和，即Math.max(root, root+left, root+right)
  function dfs(node){
    if (!node) return 0;

    //计算左边分支最大值，左边分支如果为负数还不如不选择
    const left = Math.max(0, dfs(node.left));
    //计算右边分支最大值，右边分支如果为负数还不如不选择
    const right = Math.max(0, dfs(node.right));

    // 情况一：left + root + right 作为路径与已经计算过历史最大值做比较
    max = Math.max(max, left + right + node.val);

    // 情况二、三:返回经过root的单边最大分支给当前root的父节点计算使用
    return Math.max(left, right) + node.val;
  }
};

654. 最大二叉树

654. 最大二叉树
0429，mid，quick
思路和 105. 106. 相似，可以一起复习
优化点：找最大值是 O(n) 的复杂度，二分法可以优化为 O(logn)。
时间复杂度：最大值+递归 == 时间复杂度：O(n^2)，可以优化为 O(nlogn)。

var constructMaximumBinaryTree = function (nums) {
  if (!nums) return null;
  return build(0, nums.length - 1);

  // 返回：构建好的子树
  function build(start, end) {
    // 边界
    if (start > end) return null;

    // 找最大值和下标
    let maxIndex = start;
    let maxVal = nums[start];
    for (let i = start; i <= end; i++) {
      if (nums[i] > maxVal) {
        maxVal = nums[i];
        maxIndex = i;
      }
    }
    // 创建节点
    const root = new TreeNode();
    root.val = maxVal;
    // 分割
    root.left = build(start, maxIndex - 1);
    root.right = build(maxIndex + 1, end);
    return root;
  }
};

617. 合并二叉树

617. 合并二叉树
0429，easy，answer
dfs 方法较为好理解，bfs 可以暂时不看了

方法一：dfs

var mergeTrees = function (root1, root2) {
  return dfs(root1, root2);

  function dfs(node1, node2) {
    // 返回，如果两个数都不存在这个节点，则返回 null
    if (!node1 && !node2) return null
    
    // 有一个不存在，则不用再判断相加，直接吧另一个存在的子树附到node即可。
    if (!node1) return node2;
    if (!node2) return node1;
    // 新建节点
    const node = new TreeNode();
    node.val = node1.val + node2.val;
    node.left = dfs(node1.left, node2.left);
    node.right = dfs(node1.right, node2.right);
    return node;
  }
};

// 优化：
var mergeTrees = function (root1, root2) {
  // 返回，如果两个数都不存在这个节点，则返回 null
  if (!root1 && !root2) return null

  // 有一个不存在，则不用再判断相加，直接吧另一个存在的子树附到node即可。
  if (!root1) return root2;
  if (!root2) return root1;
  // 新建节点
  const node = new TreeNode(root1.val + root2.val);
  node.left = mergeTrees(root1.left, root2.left);
  node.right = mergeTrees(root1.right, root2.right);
  return node;
};

时间 / 空间复杂度：O(min(m,n))，主要取决于节点数更少的那个二叉树。

方法二：bfs

不好理解，复习时暂时忽略吧；
时间复杂度、空间复杂度和 dfs 相同。

var mergeTrees = function (root1, root2) {
  // 边界
  if (root1 === null) return root2;
  if (root2 === null) return root1;

  const root = new TreeNode(root1.val + root2.val);
  const queue = [[root, root1, root2]];

  // bfs
  // 与传统思维不同，在每次push node的时候，已经处理了node.val，需要处理的是 node.left 和 node.right
  while (queue.length) {
    const [node, node1, node2] = queue.shift();

    // 左子树
    if (node1.left || node2.left) {
      if (node1.left && node2.left) {
        node.left = new TreeNode(node1.left.val + node2.left.val);
        queue.push([node.left, node1.left, node2.left]);
      } else {
        node.left = node1.left || node2.left;
      }
    }
    // 右子树
    if (node1.right || node2.right) {
      if (node1.right && node2.right) {
        node.right = new TreeNode(node1.right.val + node2.right.val);
        queue.push([node.right, node1.right, node2.right]);
      } else {
        node.right = node1.right || node2.right;
      }
    }
  }
  return root;
}

5. 最长回文串​

解法一：动态规划​

解法二：分类讨论​

105. 从前序与中序遍历序列构造二叉树​

106. 从中序与后序遍历序列构造二叉树​

107. 二叉树的层序遍历 II​

102. 二叉树的层序遍历​

103. 二叉树的锯齿形层序遍历​

199. 二叉树的右视图​

解题一：广度优先​

解法二：深度优先​

637. 二叉树的层平均值​

解法一：广度优先​

解法二：深度优先​

429. N 叉树的层序遍历​

515. 在每个树行中找最大值​

116. 填充每个节点的下一个右侧节点指针​

117. 填充每个节点的下一个右侧节点指针 II​

优化：内存优化​

104. 二叉树的最大深度​

方法一：深度优先​

方法二：广度优先​

111. 二叉树的最小深度​

方法一：广度优先 bfs​

方法二：深度优先 dfs​

226. 翻转二叉树​

方法一：dfs 递归​

方法二：bfs 迭代​

144. 二叉树的前序遍历​

方法一：递归​

方法二：迭代​

方法三：通用迭代​

145. 二叉树的后序遍历​

方法一：递归​

方法二：迭代​

方式三：统一迭代​

94. 二叉树的中序遍历​

方法一：递归​

方法二：迭代​

方法三：统一迭代​

101. 对称二叉树​

方法一：递归​

方法二：栈迭代​

方法三：队列迭代​

559. N 叉树的最大深度​

方法一：bfs 迭代​

方法二：dfs 递归​

方法三：dfs 迭代​

222. 完全二叉树的节点个数​

方法一：dfs​

方法二：利用完全二叉树特点​

110. 平衡二叉树​

257. 二叉树的所有路径​

方法一：递归+回溯​

方法二：迭代​

100. 相同的树​

方式一：递归 dfs​

方法二：迭代 bfs​

方法一：递归 dfs​

方法二：迭代 bfs​

方法三：迭代 dfs​

513. 找树左下角的值​

方法一：迭代 bfs​

方法二：递归 dfs​

112. 路径总和​

方式一：dfs 递归​

方式二：dfs 迭代​

113. 路径总和 II​

方式一：dfs 递归​

方式二：bfs 迭代​

方法三：dfs 迭代 + map 优化内存​

437. 路径总和 III​

面试题 04.12. 求和路径​

方法一：自底向上求和（自己的方法）​

方法二：自顶向下求和​

方法三：前缀和​

70. 爬楼梯​

方法一：[动态规划] 正解​

方法二：优化-动态规划​

方法三：[dfs] 超时​

5. 最长回文串

解法一：动态规划

解法二：分类讨论

105. 从前序与中序遍历序列构造二叉树

106. 从中序与后序遍历序列构造二叉树

107. 二叉树的层序遍历 II

102. 二叉树的层序遍历

103. 二叉树的锯齿形层序遍历

199. 二叉树的右视图

解题一：广度优先

解法二：深度优先

637. 二叉树的层平均值

解法一：广度优先

解法二：深度优先

429. N 叉树的层序遍历

515. 在每个树行中找最大值

116. 填充每个节点的下一个右侧节点指针

117. 填充每个节点的下一个右侧节点指针 II

优化：内存优化

104. 二叉树的最大深度

方法一：深度优先

方法二：广度优先

111. 二叉树的最小深度

方法一：广度优先 bfs

方法二：深度优先 dfs

226. 翻转二叉树

方法一：dfs 递归

方法二：bfs 迭代

144. 二叉树的前序遍历

方法一：递归

方法二：迭代

方法三：通用迭代

145. 二叉树的后序遍历

方法一：递归

方法二：迭代

方式三：统一迭代

94. 二叉树的中序遍历

方法一：递归

方法二：迭代

方法三：统一迭代

101. 对称二叉树

方法一：递归

方法二：栈迭代

方法三：队列迭代

559. N 叉树的最大深度

方法一：bfs 迭代

方法二：dfs 递归

方法三：dfs 迭代

222. 完全二叉树的节点个数

方法一：dfs

方法二：利用完全二叉树特点

110. 平衡二叉树

257. 二叉树的所有路径

方法一：递归+回溯

方法二：迭代

100. 相同的树

方式一：递归 dfs

方法二：迭代 bfs

方法一：递归 dfs

方法二：迭代 bfs

方法三：迭代 dfs

513. 找树左下角的值

方法一：迭代 bfs

方法二：递归 dfs

112. 路径总和

方式一：dfs 递归

方式二：dfs 迭代

113. 路径总和 II

方式一：dfs 递归

方式二：bfs 迭代

方法三：dfs 迭代 + map 优化内存

437. 路径总和 III

面试题 04.12. 求和路径

方法一：自底向上求和（自己的方法）

方法二：自顶向下求和

方法三：前缀和

70. 爬楼梯

方法一：[动态规划] 正解

方法二：优化-动态规划

方法三：[dfs] 超时