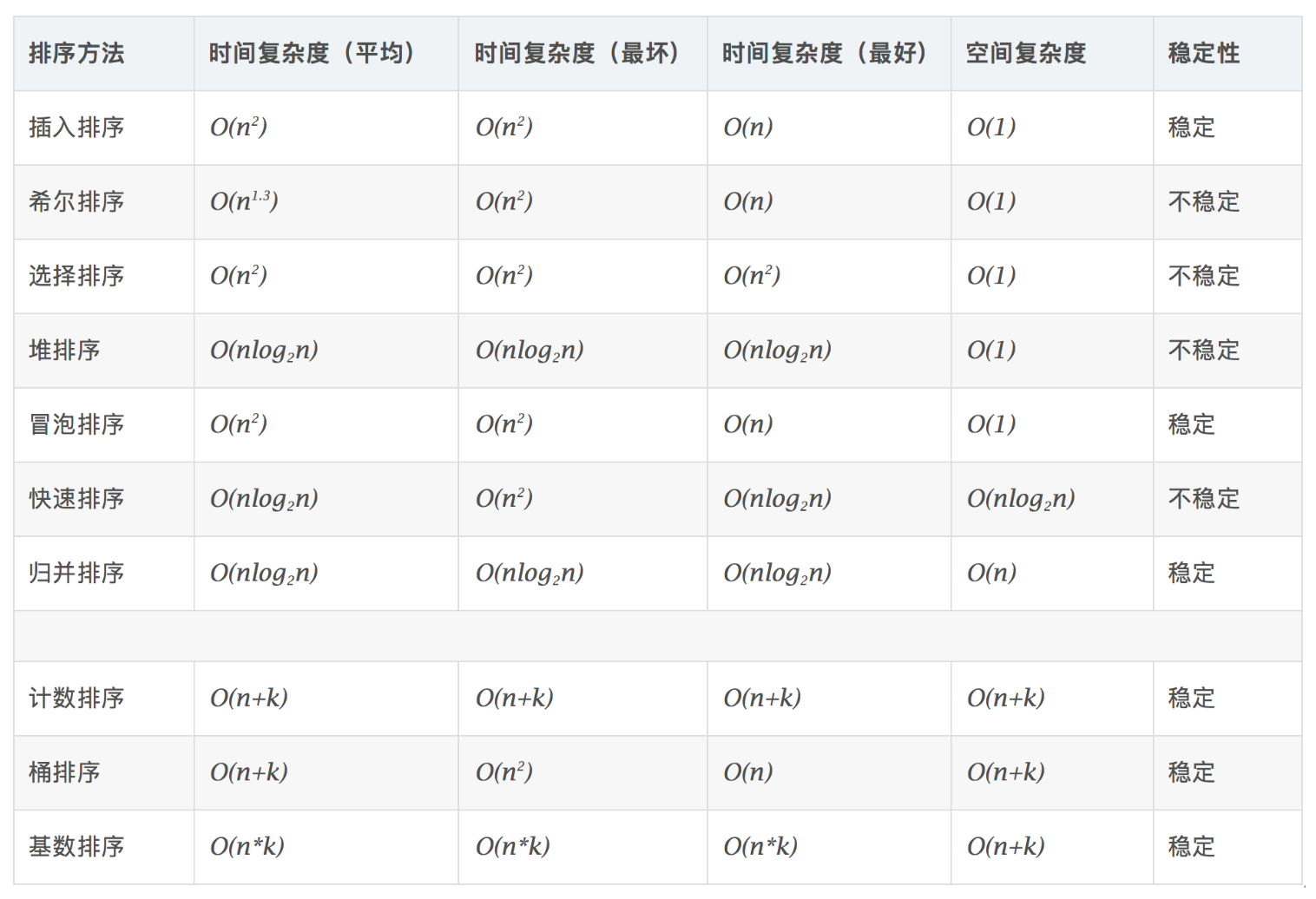
5. 排序

todo：进一步分析每个排序的特点（优点、缺点），使用场景，复杂度分析等。

1 冒泡排序（Bubble Sort）

• 每一轮排序 i 中，都会让 j 对当前位置和其后面的位置进行对比，将较大树放在后面。
• 每一轮排序，让最大的数下沉到最后一个位置。

const arr = [0, 13, 3, 16, 1, 18, 4, 15, 14, 17, 10, 9, 19, 8, 6, 11, 12, 5, 7, 2];

bubbleSort(arr);
function bubbleSort(arr) {
  for (let i = 0; i < arr.length; i++) {
    for (let j = 0; j < arr.length - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }
  return arr;
}

2. 选择排序（Selection Sort）

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

• 每一轮 i 循环，找到当前最小值 minIndex，然后和该轮头交换位置。

function selectionSort(arr) {
    for (let i = 0; i < arr.length; i++) {
        let minIndex = i;
        for (let j = i + 1; j < arr.length; j++) {
            if (arr[j] < arr[minIndex]) minIndex = j;
        }
        [arr[i], arr[minIndex]] = [arr[minIndex], arr[i]];
    }
    return arr;
}

• 特点：最直观，表现最稳定，无论什么数据都是 O(n^2) 时间复杂度。

3 插入排序（Insertion Sort）

维护一个有序序列，在相应位置中，不断的插入新数据。【原地修改，只移动数组】

• 第一个元素狗构成一个有序序列。
• 接下来的元素不断往前对比，直到找到合适的位置插入。

function insertionSort(arr) {
  // 从 1 开始，下标0默认是一个有序队列
  for (let i = 1; i < arr.length; i++) {
    let preIndex = i - 1; // preIndex 最初指向有序队列的队尾
    const target = arr[i]; // target 当前待插入的值
    while (preIndex >= 0 && arr[preIndex] > target) {
      arr[preIndex + 1] = arr[preIndex]; // preIndex 值往后移动，空出当前位置
      preIndex--;
    }
    arr[preIndex + 1] = target;     // 找对地方放入 target
  }
  return arr;
}

4 希尔排序（Shell Sort）

1959年 Shell 发明，第一个突破 O(n^2) 的排序算法，是简单插入排序的改进版。🔗

• 对数组进行分组，每个分组内部进行插入排序
• 最初每个分组的长度为2，分组数量为 len / 2；最终分组长度为 len，分组数量为1。
• 分组采用间隔分组，同一个组内的成员互相都不挨着。

分组：

假设 len = 20；
第一组：10 - 20；
第二组：5 - 20；
第三组：2 - 20；
第四组：1 - 20；

代码:

function shellSort(arr) {
  const len = arr.length;
  // gep 每次减少一半: 10, 5, 2, 1
  for (let gap = Math.floor(len / 2); gap > 0; gap = Math.floor(gap / 2)) {
    // gap的长度 == 分组的数量
    // 从i=gap开始，对每个分组的第一位进行插入算法，然后对每个分组的第二位进行插入算法，以此类推。
    // 并不是先对分组1完全计算完毕，再计算分组2。
    for (let i = gap; i < len; i++) {
      let j = i;
      const target = arr[i];
      while (j >= gap && target < arr[j - gap]) {
        arr[j] = arr[j - gap];
        j = j - gap;
      }
      arr[j] = target;
    }
  }
  return arr;
}

5 归并排序（Merge Sort）

分治法（Divide and Conquer），以空间换时间。

• 2路归并。将数组切分为两个子数组，然后各自再进行并归操作，最后将数组然后合并。
• 末端：递归的返回值是切分的数组长度为1。
  • 所以 merge(left, right) 最初执行时，left 和right 的长度一定为 1。
  • 所以，merge 中 left 和 right 两个数组，各自内部是一定按序的。
  • merge 的算法就是从 left 和 right 的左侧以此取出更小的值，放入 sorted 中，最终返回 sorted。

function mergeSort(arr) {
  // 边界
  if (arr.length <= 1) return arr;
  // 数组切分
  const mid = Math.floor(arr.length / 2);
  const left = arr.slice(0, mid);
  const right = arr.slice(mid);
  // 递归
  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  const sorted = [];
  // 从 left 和 right 的第一个成员开始判断：谁更小，就取出放入 sorted 中。
  // 注意，为了确保有序，left[0] <= right[0]。
  while (left.length > 0 && right.length > 0) {
    left[0] <= right[0] 
      ? sorted.push(left.shift()) 
        : sorted.push(right.shift());
  }
  // 如果left和right有一个数组为空，则把另一个（都更大）全部放入sorted中。
  while (left.length) sorted.push(left.shift());
  while (right.length) sorted.push(right.shift());
  return sorted;
}

6 快速排序（Quick Sort）

// 原生API: sort() 将元素转换为字符串，然后按照 UTF-16 进行排序。
// 即使数组内容全部是 number，也会转化为 string 然后再进行比较。
["c","b","a","A","C","B",3,2,1].sort()      // (9) [1, 2, 3, 'A', 'B', 'C', 'a', 'b', 'c']

// 快速排序 1
function quickSort(arr) {
    let left = 0, right = arr.length - 1;
    main(arr, left, right);
    return arr;
  
    function main(arr, left, right) {
        if (arr.length === 1) return;
        let index = partition(arr, left, right);

        if (left < index - 1) main(arr, left, index - 1);
        if (index < right)    main(arr, index, right);
    }

    function partition(arr, left, right) {
        let pvoit = arr[Math.floor((left + right) / 2)];  // 取开头会非常慢

        while (left <= right) {
            while (arr[left] < pvoit) left++;
            while (arr[right] > pvoit) right--;

            if (left <= right) {
                [arr[left], arr[right]] = [arr[right], arr[left]];
                left++;
                right--;
            }
        }
        return left;
    }
}

let arr = [5, 43, 7, 60, 5, 3, 21, 8, 1];
console.log(quickSort(arr));

7 堆排序（Heap Sort）

堆 Heap 是一个完全二叉树：

• 大顶堆：每个结点的值都大于或等于其左右孩子结点的值；
• 小顶堆：每个结点的值都小于或等于其左右孩子结点的值。

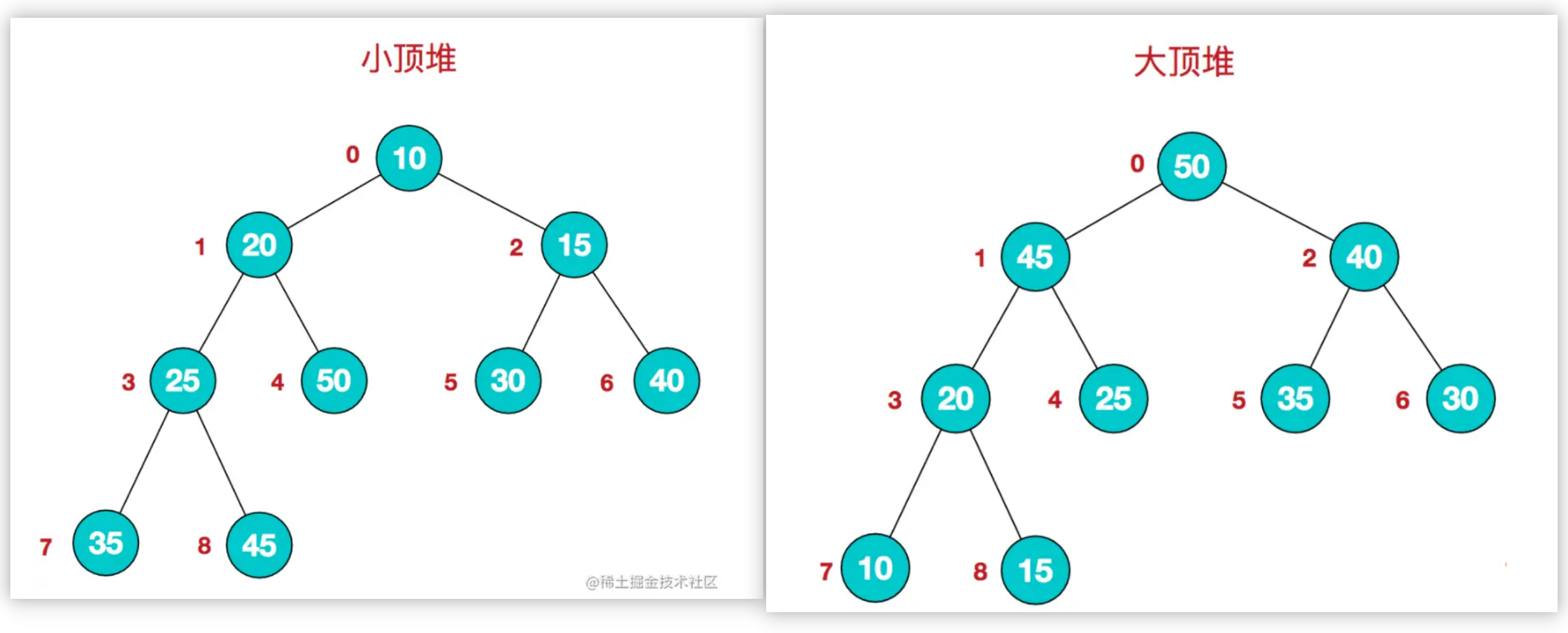
如需要升序排列，维护一个大顶堆即可。

1. 放入：将数组中成员以此放入大顶堆中，更新大顶堆结构。
2. 取出：每次取出大顶堆中的根结点，根节点即为数组中最大的元素。取出后更新大顶堆结构。

// 预备知识：
如果用一个数组表示二叉树：
-- 节点 n 的左子节点：2*n + 1;
-- 节点 n 的右子节点：2*n + 2;
-- 节点 n 的父节点：Math.floor((n-1)/2)
树的最后一个非叶子节点： Math.floor(nums.length / 2) - 1

// 构建操作
1. 递归思路。
2. 循环：第一次建堆时，遍历数组中左侧的一半元素（找到最后一个父节点）
        --- middle 是当前堆中的最后一个非叶子节点（最后一个父节点）；
        --- 同时要中间向左侧倒序遍历，这样才能保证把最大的元素移动到数组头部。
3. 在每次递归中，找到：父节点、左孩子、右孩子中的最大值，然后交换到父节点位置。
4. 如果发生交换，继续递归：
        --- 假设父节点和左孩子交换。左孩子换成了更小值，为了确保左孩子比它孩子要大，则向下递归。

// 排序操作
1. 把最大值（arr[0]）与未排序部分的最后一个元素交换，剩余的部分重新构建堆顶堆。


// 插入操作（这里用不到）
1. 将带插入节点 x 放入数组末端，也就是二叉树最后一个叶子节点。
2. 将节点 x 和父节点进行比较，较大值才能做父节点。
3. 循环，如果父节点和x节点发生替换，则重复2，继续和父节点交换位置，直到root节点。

代码：

function heapSort(arr) {
  // 构建大顶堆：i 从最后一个父节点，从下往上遍历
  for (var i = Math.floor(arr.length / 2); i >= 0; i--) {
    heapify(i, arr.length - 1);
  }

  // arr[0] 是大顶堆中root，为最大值。
  // arr[i] 是未排序序列中最后一个位置。 [0, i] 是大顶堆，[i+1, len - 1] 是递增序列
  for (let i = arr.length - 1; i > 0; i--) {
    [arr[0], arr[i]] = [arr[i], arr[0]];
    // 交换后，位置 i 
    heapify(0, i - 1);
  }
  return arr;

  // 调整大顶堆：找到最大值，并交换位置到父节点，然后递归
  // [0, range] 闭区间，代表大顶堆要调整的范围
  function heapify(rootIndex, range) {
    let largestIndex = rootIndex;
    const left = 2 * rootIndex + 1;
    const right = 2 * rootIndex + 2;

    // 找到最大值
    if (left <= range && arr[left] > arr[largestIndex]) largestIndex = left;
    if (right <= range && arr[right] > arr[largestIndex]) largestIndex = right;
    // 如果最大值不是root，交换 + 向下递归
    if (largestIndex !== rootIndex) {
      [arr[largestIndex], arr[rootIndex]] = [arr[rootIndex], arr[largestIndex]];
      heapify(largestIndex, range);
    }
  }
}

8 计数排序（Counting Sort）

适用于小范围树，且最大最小值已知的排序。

1. 已知：数组中数字的范围：最大值、最小值。
2. 利用数据结构（array），统计每个值在数组中出现的次数，填入对应数组位置中。
3. 利用数组统计结果，还原为一个有序数列。

function countingSort(arr, maxValue) {
  // 统计
  const set = new Array(maxValue + 1).fill(0);
  for (const num of arr) {
    set[num]++;
  }
  // 依次放入，直到 set 中对应元素统计值为0
  let sortedIndex = 0;
  for (let i = 0; i < set.length; i++) {
    while (set[i] > 0) {
      arr[sortedIndex] = i;
      sortedIndex++;
      set[i]--;
    }
  }
  return arr;
}

9 桶排序（Bucket Sort）

计数排序的升级版。假设输入数据均匀分布，将数据分到有限数量的桶里，每个桶各自排序（使用其他排序算法，或是递归使用桶排序）。🔗

function bucketSort(arr, bucketSize = 5) {
  if (arr.length === 0) return arr;
  // 最值
  const min = Math.min(...arr);
  const max = Math.max(...arr);
  // 桶：初始化。buckets 二维数组，保存了所有桶。
  const count = Math.floor((max - min) / bucketSize) + 1;
  const buckets = Array.from(new Array(count), () => new Array());
  // 将数据分配到各个桶中
  for (let i = 0; i < arr.length; i++) {
    buckets[Math.floor((arr[i] - min) / bucketSize)].push(arr[i]);
  }
  // 对各个桶使用插入排序，然后结果合并到 sorted中
  const sorted = [];
  buckets.forEach((item) => {
    radixSort(item);  // 这里使用了插入排序，也可以用其他方式
    sorted.push(...item);
  });
  return sorted;
}

10 基数排序（Radix Sort）

🪣基于桶的排序思想 🔗。

1. 划分为 0-9 十个桶，每个桶都是栈结构。分多次装入 / 取出。
2. 第一次：所有数字只看个位数，然后依次放入对应的桶中。
   • 放入后，再从 0-9 依次把桶中的数字取出，放回数组中。
   • 此时：数组中所有成员是按照个位数从 0 - 9 递增排序的。
3. 第二次：复用步骤 2 的逻辑，所有数字只看十位数，放入对应的桶中。
4. 递归，直到排序完毕

function radixSort(arr) {
  // 最大值：最大值的位数 == 遍历次数
  const max = Math.max(...arr);
  // 定义桶
  const buckets = Array.from({ length: 10 }, () => []);
  // 当前遍历位数：个位、十位、百位.
  for (let m = 1; m < max; m *= 10) {
    // 放入桶
    arr.forEach((number) => {
      // digit表示某位数的值
      const digit = ~~((number % (m * 10)) / m);

      // 把该位数的值放到桶buckets中
      // 通过索引确定顺序 类比计数排序
      // @ts-ignore
      buckets[digit].push(number);
    });
    // 从桶buckets中取值
    // 完成此步后 就完成了一次位数排序
    let ind = 0;
    buckets.forEach((bucket) => {
      while (bucket.length > 0) {
        // shift从头部取值
        // 保证按照队列先入先出
        arr[ind++] = bucket.shift();
      }
    });
  }
  return arr;
}

引用：

• 部分内容不准确：🔗